元宵灯笼其实是要这样玩的!
我是焦慧,就是NCC自然课的子悦妈妈。这是NCC的公号,请关注,谢谢!
NCC(Nature Connection in City)呼吁人们了解自己的城市,看见身边的自然,师从自然,思考人与自然的关系。带孩子一起和自然建立联结,收获的将远不止是心灵手巧身强体壮,而是整个人的全面成长,包括我们自己。
CITY节庆:今年元宵,特别需要点亮灯笼
很快就有小朋友发来成品图,元宵当晚,更多手折灯笼在朋友圈亮相,让我们不出门也云赏灯了。
以下是部分朋友分享的图片:
最高效的淼淼同学作品(上、下)
这是小苹果同学的“祈福灯”
这是Ivy分享的作品“图腾灯”,作者不知道是哥哥还是弟弟?
小苹果同学家的2.0版放光啦!
这是六六和九九姐弟的作品
这是飞飞同学旧物利用版,连挂绳和推拉扣都做了改造。
这是子悦家的作品,三角形的拼接方式不同,亮灯后的花纹就不同。
感谢以上朋友的分享!所以,大家发现了吗?
虽然大家都是看同一个教程,作品却都是非常独特的。
除了材料的尺寸和颜色之外,每件作品还有很多其他的不同。
因为在制作的过程中,每个人都遇到了“问题”。
大家的“问题”不同,“解决方案”也不同;
再加上,每位作者都愿意加一点自己的灵感和创意。
如此一来,
“问题”+“”解决方案+“改造”=独一无二的作品!!!
这就是NCC手工课的用意。
即使没有与大家聚在一起动手,
也不想缺席手工背后的小解析。
请回顾一下动手的过程,
你遇到了哪些问题?
你是如何解决的?
你加入了哪些自己的小创意?
也许你或者孩子有过以下问题,
也许你该根据孩子的年龄和兴趣方向等,
问问以下问题。
问题还能列很多,解答方式就更多!
只要你亲手做过,你就会发现,很多问题都不难解决。
本文开头的那些作品中就能发现上图大部分的问题答案。
以下举例给出几个“解决方案”吧:
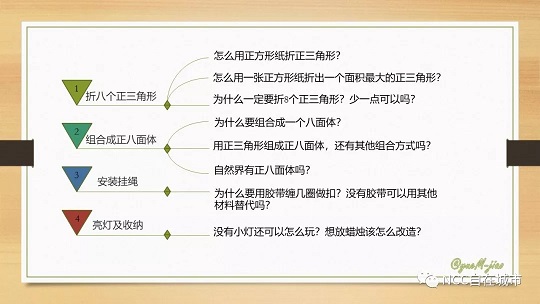
问题一:怎么用正方形折正三角形?
解决方案:1、可以用三角板,或者量角器和直尺,在正方形纸上画出正三角形,再剪下来。此方法特别适合厚一些的铜版纸、卡纸、刮画纸、纸皮等。
2、画的方法还有圆规、直尺法哦。
3、材料充足的情况下,可以用三条等长的小木棍、筷子、吸管等,两两固定,组合成三角形的框架。中间用硫酸纸、花纸、纱等贴合。如此完成一个正三角形单体。
4、没有三角板,不会用圆规,也没有可以做骨架的材料的话,当然是用教程里的方法啦!再复习一遍: 上图的原理其实就是代替了圆规,在正方形内做出一个正三角形。
怎么证明这就是正三角形?请爸爸妈妈帮你证明一下!
连同下面的一起证明一下哈!
问题二:
怎么用一张正方形纸折出一个面积最大的正三角形?
解决方案:看图!
这个方法步骤少,折出来的三角形又大,为什么焦老师不用它做灯笼单体呢?怎么用一张正方形纸折出一个面积最大的正三角形?
因为立体结构还要考虑纸张厚度,用教程里的方法,纸张折叠的部分最多处有4层,很适合做挂绳部分,解决了被戳洞易损坏的问题。
问题三:
为什么一定要折8个正三角形?少一点可以吗?
解答:为什么一定要折8个正三角形?少一点可以吗?
1、此次的灯笼设计为可折叠收纳型,所以选取了正八面体的结构。正八面体就需要有8个正三角形组成。
2、如果只考虑能不能少折几个正三角形的话,4个正三角形就可以构成一个立体结构啦,即正四面体。
而6个正三角形也可以组合成一个立体结构。
但是以上两种灯笼不方便折叠收纳,因为中心是三角形结构。
其实,如果要用纸折六面体的话,端午手工教过大家的彩粽的内芯更简便啦,对不对!
那么正六面体又是什么样子呢?原来就是立方体呀!
说再多都不如动手一试来得真切哦!试试吧!
问题四:为什么要组合成一个八面体?
解答:已经被上面抢答啦!
问题五:
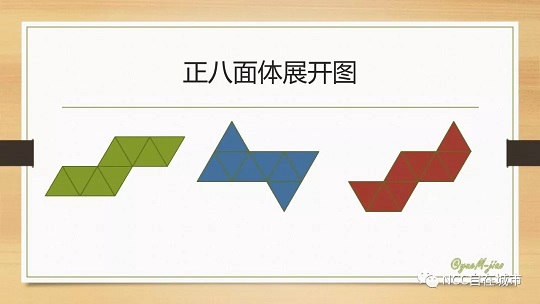
用正三角形组成正八面体,还有其他方式吗?
解答:看图!
也就是说,只要你把8个正三角形按照上图的方式拼接起来,都可以组合成一个正八边形的灯笼哦!用正三角形组成正八面体,还有其他方式吗?
——“原来做手工是假,学数学是真!?”
——“难道你不觉得有趣才是真吗?!”
问题还没回答完,
问题永远回答不完。
因为只要你“玩”起来,
就停不下来了!
元宵节过完了,疫情拐点还没出现,
大家可以继续做八面体,六面体,四面体……
材料不够,就把做好的灯笼拆了,
再换个方式组装吧!
祝大家:玩手工,学得开心呀!
(留言功能会尽快开通,欢迎大家用各种方式继续和我交流!邮箱:2727708@qq.com)
NCC 自在城市